Java/Coding Test
[코딩테스트] 소수(에라토스테네스 체)
Jane Kwon
2022. 3. 7. 23:00
반응형
문제
자연수 N이 입력되면 1부터 N까지의 소수의 개수를 출력하는 프로그램을 작성하세요.
만약 20이 입력되면 1부터 20까지의 소수는 2, 3, 5, 7, 11, 13, 17, 19로 총 8개입니다.
입력
첫 줄에 자연수의 개수 N(2<=N<=200,000)이 주어집니다.
출력
첫 줄에 소수의 개수를 출력합니다.
예시 입력
20예시 출력
8
문제 풀이
[첫번째 풀이]
import java.util.Scanner;
public class Main {
public int solution(int num) {
int count = 0;
for (int i=2; i<=num; i++) {
boolean d = true;
for (int j=2; j<i; j++) {
if (i%j == 0) {
d = false;
break;
}
}
if (d) count++;
}
return count;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int num = scanner.nextInt();
Main main = new Main();
System.out.println(main.solution(num));
}
}(Time 1507ms / Memory 27MB) Time Limit Exceeded
[두번째 풀이]
import java.util.Scanner;
public class Main {
public int solution(int num) {
int count = 0;
int[] array = new int[num + 1];
for (int i=2; i<=num; i++) array[i] = i;
for (int i=2; i<=num; i++) {
if (array[i] == 0) continue;
for (int j=i*i; j<=num; j+=i) array[j] = 0;
}
for (int j : array) {
if (j != 0) count++;
}
return count;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int num = scanner.nextInt();
Main main = new Main();
System.out.println(main.solution(num));
}
}(Time 173ms / Memory 28MB) Runtime Error
[세번째 풀이]
import java.util.Scanner;
public class Main {
public int solution(int count) {
int[] numbers = new int[count + 1];
for (int i=0; i<=count; i++) numbers[i] = i;
for (int i=2; i<numbers.length; i++) {
if (numbers[i] == 0) {
continue;
}
for (int j=i+i; j<numbers.length; j+=i) numbers[j] = 0;
}
count = 0;
for (int i=2; i<numbers.length; i++) {
if (numbers[i] != 0) count++;
}
return count;
}
public static void main(String[] args){
Scanner scanner = new Scanner(System.in);
int count = scanner.nextInt();
Main main = new Main();
System.out.println(main.solution(count));
}
}(Time 163ms / Memory 28MB)
- 첫번째 풀이처럼 풀었는데 Time Limit Exceeded가 떨어졌다.
- 두번째 풀이부터는 에라토스테네스 체에 대해 알아본 후 그 방식대로 코드를 짜봤는데 두번째 풀이는 Runtime Error가 떨어졌다. 왜지?
- 마음을 다잡고 다시 한번 에라토스테네스 체 방식으로 풀어본 후 드디어 정답을 받았다.
* 에라토스테네스의 체
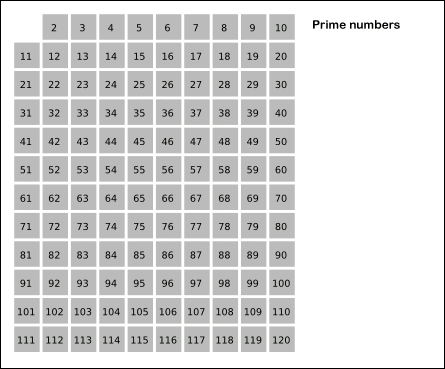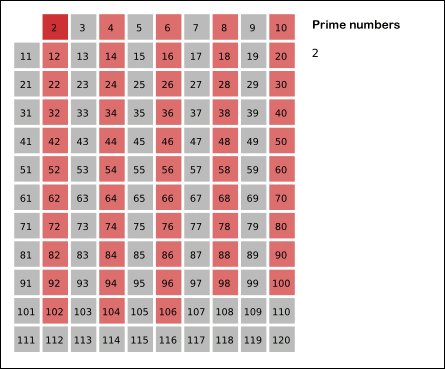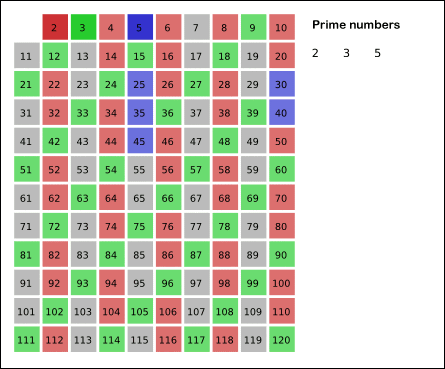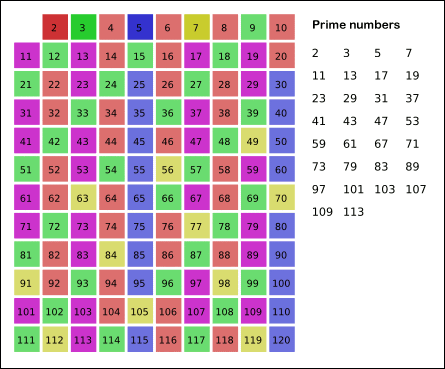
2부터 시작해서 본인을 제외한 배수 값을 전부 제거해내가는 방식으로 소수를 걸러내는 방식이다.
반응형